解：⑴由题意，a+b+c=2，

∵a=1，∴b+c=1，

物线顶点为A，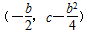

设B（x₁，0），C（x₂，0），

∵x₁+x₂=-b，x₁x₂=c，△=b²-4c＞0，

∴|BC|=|x₁-x₂|=，

∵△ABC为等边三角形，

∴，

即，

∵b²-4c＞0，

∴，

∵c=1-b，

∴b²+4b-16=0，b=-2±2，

所求b值为-2±2；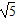

⑵∵a≥b≥c，若a＜0，则b＜0，c＜0，a+b+c＜0，与a+b+c=2矛盾，

∴a＞0，

∵b+c=2-a，bc=，

∴b、c是一元二次方程x²-（2-a）x+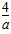=0的两实根，

∴△=（2-a）²-4×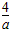≥0，

∴a³-4a²+4a-16≥0，即（a²+4）（a-4）≥0，故a≥4，

∵abc＞0，

∴a、b、c为全大于0或一正二负，

①若a、b、c均大于0，∵a≥4，与a+b+c=2矛盾；

②若a、b、c为一正二负，则a＞0，b＜0，c＜0，则|a|+|b|+|c|=a-b-c=a-（2-a）=2a-2，

∵a≥4，故2a-2≥6，

当a=4，b=c=-1时，满足题设条件且使不等式等号成立，故|a|+|b|+|c|的最小值为6。