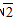（1）由BC=1，AB=2，cosB=

1

4

，

根据余弦定理可得：AC²=AB²+BC²-2AB•BCcosB=4+1-2×2×1×

1

4

=4，

开方得：AC=2；

（2）由cosB=

1

4

，且B为三角形的内角，

可得：sinB=

1-cos2B

=

15

4

，又BC=1，AB=2，

∴S_△ABC=

1

2

AB•BC•sinB=

1

2

×2×1×

15

4

=

15

4

．