（1）∵圆O₁的方程为：（x+2）²+y²=1，

∴圆O₁的圆心为（-2，0），半径r₁=1；同理圆O₂的圆心为（2，0），半径r₂=7．

设动圆的半径为R、圆心为M，圆M与圆O₁外切于点E，圆M与圆O₂内切于点F，连结O₁M、O₂F，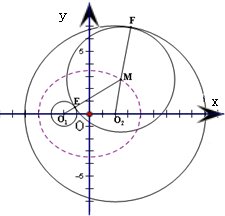

则E点在O₁M上，M在O₂F上．

∵|O₁M|=|O₁E|+|EM|，|O₂M|=|O₂F|-|MF|，

∴|O₁M|=r₁+R，|O₂M|=r₂-R，

两式相加得：|O₁M|+|O₂M|=r₁+r₂=1+7=8（定值），

∴圆心M在以O₁、O₂为焦点的椭圆上运动，

由2a=8，c=2，得a=4，b=

a2-c2

=2

3

，

椭圆方程为

x2

16

+

y2

12

=1．

即动圆圆心的轨迹方程为C：

x2

16

+

y2

12

=1；

（2）直线OA的斜率为k=

3-0

2-0

=

3

2

，则平行于OA的直线l的斜率也是

3

2

，

假设存在符合题意的直线l，设其方程为y=

3

2

x+t，

由

y= 3 2 x+t x2 16 + y2 12 =1

消去y，得3x²+3tx+t²-12=0，

∵直线l与椭圆有公共点，

∴△=（3t）²-4×3×（t²-12）≥0，解得-4

3

≤t≤4

3

，

另一方面，由直线OA：

3

2

x-y=0与l：

3

2

x-y+t=0的距离为

|t|

( 3 2 )2+(-1)2

=4，解之得t=±2

13

，

由于±2

13

∉[-4

3

，4

3

]，所以符合题意的直线l不存在．