问题
解答题
已知动点P（x，y）与两定点M(-1，0)，N(1，0)连线的斜率之积等于常数λ（λ≠0）。
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ）试根据λ的取值情况讨论轨迹C的形状：
（Ⅲ）当λ=-2时，过定点F(0，1)的直线l与轨迹C交于A、B两点，求△AOB的面积的最大值。
答案
解：（Ⅰ）由题设知直线PM与PN的斜率存在且均不为零，
所以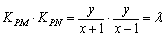
，
整理得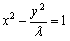
（λ≠0，x≠±1）。
（Ⅱ）①当λ＞0时，轨迹C为中心在原点，焦点在x轴上的双曲线（除去顶点）；
②当-1＜λ＜0时，轨迹C为中心在原点，焦点在x轴上的椭圆（除去长轴两个端点）；
③当λ=-1时，轨迹C为以原点为圆心，1的半径的圆除去点(-1，0)，(1，0)；
④当λ＜-1时，轨迹C为中心在原点，焦点在y轴上的椭圆（除去短轴的两个端点）。
（Ⅲ）当λ=-2时，轨迹C为椭圆
（x≠±1） ，
由题意知，l的斜率存在，设l的方程为y=kx+1，
代入椭圆方程中整理，得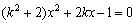
， （*）
设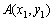
，
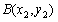，则x1，x2的方程（*）的两个实根，
∴
，
，
∴ 
，
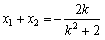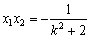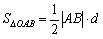
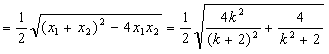
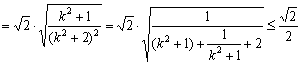当k=0时，取“=”，
∴k=0时，△OAB的面积取最大值为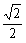
。