问题
单项选择题
已知直线y=k(x+2)(k＞0)与抛物线C：y2=8x相交A、B两点，F为C的焦点．若|FA|=2|FB|，则k=（）．
A.A
B.B
C.C
D.D
答案
参考答案：D
解析：
抛物线y2=8x的准线为x=-2.直线y=k(x+2)(k＞0)恒过定点P(-2，0)．如下图所示过点P作直线l：x=-2，过点A、B分别作直线l的垂线，垂点为M、N.
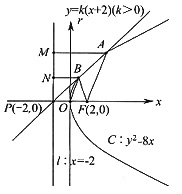
由|FA|=2|FB|得：|AM|=2|BN|．点B为AP的中点、连接OB，则
，∴|OB|=|BF|，点B的横坐标为1，故点B的坐标为
∴
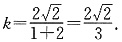故选D．