问题
解答题
在平面直角坐标系xOy中，点P到点F（3，0）的距离的4倍与它到直线x=2的距离的3倍之和记为d，当P点运动时，d恒等于点P的横坐标与18之和，
（Ⅰ）求点P的轨迹C；
（Ⅱ）设过点F的直线l与轨迹C相交于M，N两点，求线段MN长度的最大值。
答案
解：（Ⅰ）设点P的坐标为（x，y），
则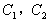
，
由题设当x＞2时，
由①得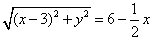
，
化简得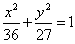
；
当x≤2时，由①得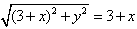
，
化简得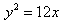
；
故点P的轨迹C是椭圆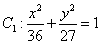
在直线x=2的右侧部分
与抛物线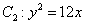
在直线x=2的左侧部分
（包括它与直线x=2的交点）所组成的曲线，参见图1；
（Ⅱ）如图2所示，易知直线x=2与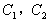的
交点都是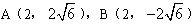
，
直线AF，BF的斜率分别为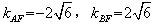
，
当点P在C1上时，由②知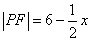
，④
当点P在C2上时，由③知|PF|=3+x，⑤
若直线l的斜率k存在，则直线l的方程为y=k（x-3），
（1）当k≤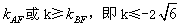
时，
直线l与轨迹C的两个交点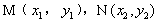
都在C1上，
此时由④知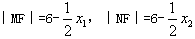
，
从而∣MN∣=∣MF∣+∣NF∣
=
，
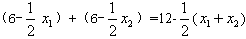由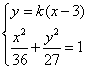
得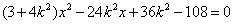
，
则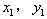
是这个方程的两根，
所以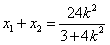
*
∣MN∣=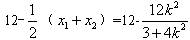
，
因为当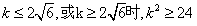
，
，
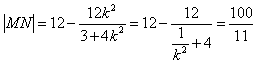当且仅当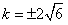
时，等号成立。
（2）当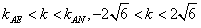
时，
直线l与轨迹C的两个交点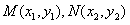
分别在
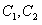上，
不妨设点M在C1上，点C2上，
则④⑤知，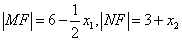
，
设直线AF与椭圆C1的另一交点为E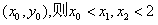
，
，
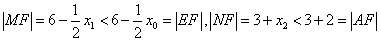所以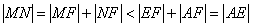
，
而点A，E都在C1上，且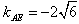
，
有（1）知
，
若直线l的斜率不存在，则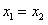
=3，
此时，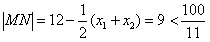
；
综上所述，线段MN长度的最大值为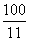
。
