若f(x)是连续函数，则下述命题正确的是( ) A．若f(x)为奇函数，则f(x)

问题单项选择题

若f(x)是连续函数，则下述命题正确的是( )

A．若f(x)为奇函数，则f(x)的任一原函数为偶函数

B．若f(x)为偶函数，则f(x)的任一原函数为奇函数

C．若f(x)满足f(x+T)=f(x)(r＞0为常数)，则f(x)任一原函数F(x)也满足F(x+T)=F(x)

D．若f(x)≤g(x)(g(x)是连续函数)，则

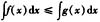
答案

参考答案：A

解析：[考点] 连续奇、偶函数，周期函数原函数的奇、偶性，周期性；不定积分的单调性
[答案解析] (A)正确，[*]因为F(x)是偶函数，c是偶函数，从而f(x)任一原函数为偶函数．
(B)不正确，[*]
(C)不正确，[*]未必是周期函数，事实上[*][F(x+T)-F(x)]=f(g+T)-f(x)=0，故F(x+T)-F(x)=c(c为任意常数)，只有c=0时，F(x)才是周期函数；c≠0时，令φ(x)=[*][*]亦即φ(x)为以T为周期函数，于是[*]必不是周期函数。
(D)不正确，定积分有单调性，即只有[*]但[*]