问题
填空题
已知恒过定点(1,1)的圆C截直线x=-1所得弦长为2,则圆心C的轨迹方程为______.
答案
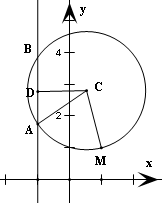
设圆心为C(x,y),定点为M(1,1),连结CM.设圆C交直线x=-1于A、B两点,
取AB的中点D,连结CD,则CD⊥AB,
∵Rt△ACD中,|CD|=x+1,|AD|=
|AB|=1,1 2
∴|AC|=
,(x+1)2+12
又∵点A、M在圆C上,可得|AC|=|MC|=
,(x-1)2+(y-1)2
∴
=(x+1)2+12
,(x-1)2+(y-1)2
两边平方,整理得y2=4x+2y,即为圆心C的轨迹方程.
故答案为:y2=4x+2y