问题
解答题
已知常数a＞0，向量c=（0，a），i=（1，0），经过原点O以c+λi为方向向量的直线与经过定点A（0，a）以i-2λc为方向向量的直线相交于点P，其中λ∈R，试问：是否存在两个定点E、F，使得|PE|+|PF|为定值，若存在，求出E、F的坐标；若不存在，说明理由。
答案
解：∵c=（0，a），i=（1，0），
∴c+λi=（λ，a），i-2λc=（1，-2λa），
因此，直线OP和AP的方程分别为λy=ax和y-a=-2λax，
消去参数λ，得点P（x，y）的坐标满足方程y（y-a）=-2a2x2，
整理得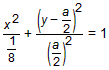
，①
因为a＞0，所以得
（Ⅰ）当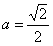
时，方程①是圆方程，故不存在合乎题意的定点E和F；
（Ⅱ）当
时，方程①表示椭圆，焦点
为合乎题意的两个定点；
（Ⅲ）当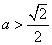
时，方程①也表示椭圆，焦点
为合乎题意的两个定点。
