问题
解答题
已知动点M(x,y)在曲线C上,点M与定点F(1,0)的距离和它到直线m:x=4的距离的比是
(1)求曲线C的方程; (2)点E(-1,0),∠EMF的外角平分线所在直线为l,直线EN垂直于直线l,且交FM的延长线于点N.试求点P(1,8)与点N连线的斜率k的取值范围. |
答案
(1)设点M到直线m:x=4的距离为d,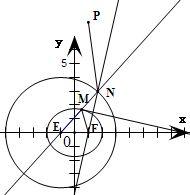
根据题意,可得
=|MF| d
,1 2
即
=(x-1)2+y2 |x-4|
,化简得1 2
+x2 4
=1.y2 3
∴曲线C的方程是
+x2 4
=1;y2 3
(2)由(1)得曲线C是E(-1,0)、F(1、0)为焦点的双曲线,2a=4.
根据题意,可知|ME|=|MN|,
∵|ME|+|MF|=2a,∴|NF|=|MN|+|MF|=4
∴点N的轨迹是以F(1,0)为圆心,4为半径的圆.
又∵直线PN的方程为:y-8=k(x-1),即kx-y+8-k=0.
∴圆心F到直线PN的距离d小于等于半径,可得
≤4,|k+8-k| k2+1
解之得k≤-
或k≥3
,可得斜率k的取值范围是(-∞,-3
]∪[3
,+∞).3
