问题
填空题
梯形的面积被一条对角线分成1：2两部分，则梯形的中位线分梯形的两部分面积之比为______．
答案
设上底长x，下底y，中位线z．
梯形的面积被一条对角线分成1：2，因为两部分的高相等，所以
=x y
，z=1 2
=x+2x 2
x．3 2
根据中位线的性质中位线分成两部分的梯形同高
÷（x+ 3x 2 2
+2x）=3x 2
．5 7
搜题请搜索小程序“爱下问搜题”
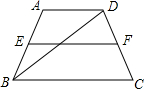
梯形的面积被一条对角线分成1：2两部分，则梯形的中位线分梯形的两部分面积之比为______．
设上底长x，下底y，中位线z．
梯形的面积被一条对角线分成1：2，因为两部分的高相等，所以
=x y
，z=1 2
=x+2x 2
x．3 2
根据中位线的性质中位线分成两部分的梯形同高
÷（x+ 3x 2 2
+2x）=3x 2
．5 7