问题
选择题
在梯形ABCD中,AB∥CD,DC:AB=1:2,E、F分别是两腰BC、AD的中点,则EF:AB等于( )
A.1:4
B.1:3
C.1:2
D.3:4
答案
∵DC:AB=1:2,
∴设DC=x,AB=2x,
∵E、F分别是两腰BC、AD的中点,
∴EF=
(AB+CD)=1 2
(2x+x)=1 2
x,3 2
∴EF:AB=
x:2x=3:4.3 2
故选D.
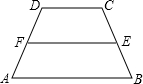
在梯形ABCD中,AB∥CD,DC:AB=1:2,E、F分别是两腰BC、AD的中点,则EF:AB等于( )
A.1:4
B.1:3
C.1:2
D.3:4
∵DC:AB=1:2,
∴设DC=x,AB=2x,
∵E、F分别是两腰BC、AD的中点,
∴EF=
(AB+CD)=1 2
(2x+x)=1 2
x,3 2
∴EF:AB=
x:2x=3:4.3 2
故选D.
