问题
填空题
一个直角梯形,两底边长为4和6,垂直于两底的腰长为2
|
答案
分为两种情况:①如图
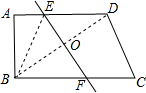
当D和B沿EF折叠重合时,OB=OD,
∵AD∥BC,
∴△DOE∽△BOF,
∴
=OE OF
,OD OB
∴OE=OF,即EF=2OE,
连接BE,
∵D和B沿EF折叠重合,
∴EF⊥BD,ED=BE,
设BE=DE=x,
则AE=4-x,在Rt△ABE中,由勾股定理得:(2
)2+(4-x)2=x2,3
解得:x=
,即DE=7 2
,7 2
在Rt△ABD中,由勾股定理得:BD=
=2(2
)2+423
,即DO=7
,7
∵在Rt△DOE中,由勾股定理得:EO=
=(
)2-(7 2
)27
,21 2
∴EF=2OE=
;21
②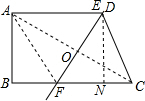
当A和C沿EF折叠重合时,过D作DN⊥BC于N,
则四边形ADNB是矩形,
BN=AD=4,CN=6-4=2,AB=DN=2
,3
在Rt△DNC中,由勾股定理得:DC=
=4=AD,(2
)2+223
即E和D重合,
连接AF,在Rt△ABF中,由勾股定理得:(2
)2+(6-AF)2=AF2,3
解得:AF=CF=4,
NF=4-2=2,
在Rt△DNF中,由勾股定理得:EF=
=4;(2
)2+223
故答案为:4或
.21

 A
A /2
/2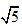 /2A
/2A