问题
解答题
已知两圆x2+y2-10x-10y=0，x2+y2+6x-2y-40=0，求
（1）它们的公共弦所在直线的方程；
（2）公共弦长。
答案
解：（1）两圆公共弦所在直线的方程为：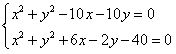
，
解得2x+y-5=0。
（2）圆
的圆心为（5，5），半径为
，
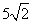圆心到公共弦的长为：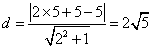
，
根据勾股定理可得公共弦的长为：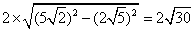
。
搜题请搜索小程序“爱下问搜题”
已知两圆x2+y2-10x-10y=0，x2+y2+6x-2y-40=0，求
（1）它们的公共弦所在直线的方程；
（2）公共弦长。
解：（1）两圆公共弦所在直线的方程为：，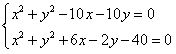
解得2x+y-5=0。
（2）圆的圆心为（5，5），半径为，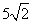
圆心到公共弦的长为：，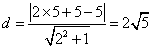
根据勾股定理可得公共弦的长为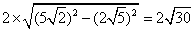：。