问题
解答题
已知圆C1：x2+y2+2x+2y-8=0与圆C2：x2+y2-2x+10y-24=0相交于A、B两点，
（1）求公共弦AB所在的直线方程；
（2）求圆心在直线y=-x上，且经过A、B两点的圆的方程．
答案
解：（1）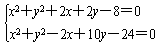
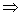x-2y+4=0．
（2）由（1）得x=2y-4，代入x2+y2+2x+2y-8=0中得，y2-2y=0，
∴
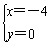或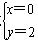
，即A（-4，0），B（0，2），
又圆心在直线y=-x上，
设圆心为M（x，-x），则|MA|=|MB|，解得M（-3，3），
∴⊙M：（x+3）2+（y-3）2=10．
