问题
单项选择题
设3×3矩阵A=(α,β1,β2),B=(β,β1,β2),其中α,β,β1,β2均为3维列向量,已知行列式|A|=2,
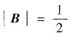 ,则行列式|A+B|=
,则行列式|A+B|=
答案
参考答案:A
解析:
[分析]: 根据行列式的性质,得
|A+B|=|α+β,2β1,β2|=|α,2β1,2β2|+|β,2β1,2β2
=22|α,β1,β2|+22|β,β1,β2|
[*]
故应选(A).
设3×3矩阵A=(α,β1,β2),B=(β,β1,β2),其中α,β,β1,β2均为3维列向量,已知行列式|A|=2,
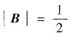 ,则行列式|A+B|=
,则行列式|A+B|=
参考答案:A
解析:
[分析]: 根据行列式的性质,得
|A+B|=|α+β,2β1,β2|=|α,2β1,2β2|+|β,2β1,2β2
=22|α,β1,β2|+22|β,β1,β2|
[*]
故应选(A).