参考答案：A

解析：

如图所示，从A点出发沿八面体的棱移动到达B位置。在移动过程中，题目要求遵守两个条件。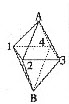

条件1，任何顶点最多到达1次；

条件2，全程必须走过所有8个面的至少1条边。

从A点出发共有4条路径(A→1，A→2，A→3，A→4)，任选一条路径A→1进行分析。

点A到点1，直线A1属于平面A14和A12。遵照条件2，从点1出发有2条路径选择(1→2，1→4)，任选一条路径1→2进行分析。

点1到点2，直线12属于平面A12和B12。遵照条件1、2，从点2出发只有一条路径选择，即2→3。

点2到点3，直线23属于平面A23和1323。遵照条件1、2，从点3出发只有一条路径选择，即3→4。

点3到点4，直线34属于平面A34和B34。遵照条件1、2，从点4出发可直接到达点B。点4到点B，直线4B属于平面B14和B34，此时走过所有8个面的至少1条边。

综上所述，该条路径A→1→2→3→4→B，符合条件1、2。且从点2开始，以后每条路径都具有唯一性。则从点A到点B共有4×2=8种不同的走法。