问题
单项选择题
利用M/M/1排队论模型分析图28-6所示的是一个简单的工作流模型（其中单位时间为1小时）。它表示这样一个执行过程：每小时将会有20个任务达到c1，这20个任务首先经过处理task1，再经过处理task2，最终将结果传递到c3。处理task1和处理task2相互独立，且每个任务到达间隔服从负指数分布。处理task1、task2的平均等待时间分别是（）。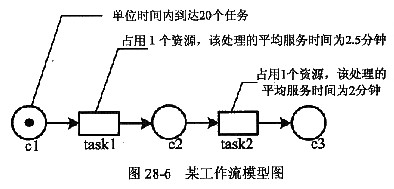
A．15分钾、6分钟
B．12.5分钟、4分钟
C．9.5分钟、5分钟
D．10分钟、3.5分钟
答案
参考答案：B
解析：
从图28-6工作流模型图可知，处理task1占用1个资源，它将接收c1在单元时间(每小时)送来的20个任务，即处理task1的每小时内到达的任务数λ=20。
由于处理task1对每个任务的平均服务时间为2.5分钟，且系统单位时间为1小时，因此处理task1的资源在单位时间内能够完成的任务数
个。
在M/M/1排队模型中，资源利用率ρ定义为平均到达任务数与平均处理任务数的比值，即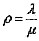
。因此，处理task1的资源利用率
。
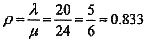处理task1的平均任务数
。
处理task1的平均系统时间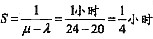
=0.25小时=0.25×60分钟=15分钟。处理task1的平均等待时间
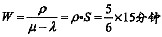=12.5分钟=0.208小时。
同理，由于“这20个任务首先经过处理task1，再经过处理task2”，因此处理task2的每小时内到达的任务数λ=20。而处理task2对每个任务的平均服务时间为2分钟，因此处理task2的资源在单位时间内的
个；处理task2的资源利用率
。
处理task2的平均任务数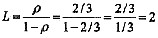
。
处理task2的平均系统时间
=0.1小时=0.1×60分钟=6分钟。
处理task2的平均等待时间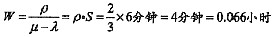
。