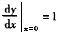问题
单项选择题
已知xey-ye-y=x2，求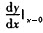
=（）
A.0
B.1
C.-1
D.2
答案
参考答案：B
解析：
当x=0时，由已知，xey-ye-y= x2，得y=0。
因为在方程等号两边分别对x求导，得
ey+xeyy′-(1-y)e-yy′=2x
将x=0，y=0代入，得
e0+0·e0y′-(1-0)e0y′=0
所以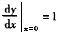
搜题请搜索小程序“爱下问搜题”
已知xey-ye-y=x2，求=（）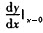
A.0
B.1
C.-1
D.2
参考答案：B
解析：
当x=0时，由已知，xey-ye-y= x2，得y=0。
因为在方程等号两边分别对x求导，得
ey+xeyy′-(1-y)e-yy′=2x
将x=0，y=0代入，得
e0+0·e0y′-(1-0)e0y′=0
所以