问题
单项选择题
设
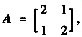B是2阶矩阵，且满足AB=B，k1，k2是任意常数，则B=
答案
参考答案：D
解析：
[分析]： 由AB=B有(A-E)B=0，因而B的列向量是齐次方程组(A-E)x=0的解．又
[*]
那么齐次方程组(A-E)x=0的基础解系是(-1，1)T，所以应选(D)．
搜题请搜索小程序“爱下问搜题”
设
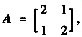B是2阶矩阵，且满足AB=B，k1，k2是任意常数，则B=
参考答案：D
解析：
[分析]： 由AB=B有(A-E)B=0，因而B的列向量是齐次方程组(A-E)x=0的解．又
[*]
那么齐次方程组(A-E)x=0的基础解系是(-1，1)T，所以应选(D)．