问题
解答题
已知一元二次方程(x﹣3)(x﹣2)﹣p2=0.
(1)当p=2时,求该方程的根;
(2)判断该方程的根的情况.
答案
解:(1)当p=2时,根据原方程,得x2﹣5x+2=0,
∴二次项系数a=1,一次项系数b=﹣5,常数项c=2,
∴△=b2﹣4ac=25﹣8=17>0,
∴x=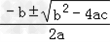 =
=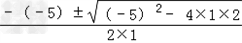 =
=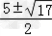 ,
,
∴x1= ,x2=
,x2=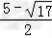 ;
;
(2)由原方程,得x2﹣5x+6﹣p2=0,
∵△=(﹣5)2﹣4×1×(6﹣p2)=1+4p2>0,
∴方程有两个不相等的实数根.
