问题
解答题
在△ABC中，a，b，c分别为内角∠A、∠B、∠C的对边，且2asinA=（2a+c）sinB+（2c+b）sinC。
（1）求∠A的大小；
（2）求sinB+sinC的最大值。
答案
解：（1）由已知，根据正弦定理，得2a2=（2b+c）b+（2c+b）c， 即a2=b2+c2+bc
由余弦定理，得a2=b2+c2-2bccosA，故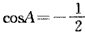
A=120°；
（2）由（1）得sinB+sinC=sinB+sin（60°-B）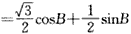
=sin（60°+B）
故当B=30°时，sinB+sinC取得最大值1。