问题
计算题
解方程：（1）2x2﹣5=4x（用配方法）；
（2）（x﹣1）（x﹣3）=1；
（3）2（x﹣2）2=x2﹣4．
答案
解：（1）移项得：2x2﹣4x=5，
二次项系数化成1得：x2﹣2x=
，
配方，得：x2﹣2x+1=
，
即（x﹣1）2=
，
则x﹣1=±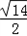
，
则x﹣1=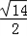
，x﹣1=﹣
．
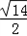则方程的解是：x1=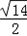
+1，x2=﹣
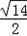+1．
（2）化成一般形式是：x2﹣4x+2=0，a=1，b=﹣4，c=2，△=16﹣4×1×2=8＞0，
则方程的解是：x=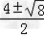
，
即x=2±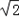
．
则x1=2+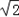
，x2=2﹣
．
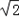（3）原式变形为：2（x﹣2）2=（x+2）（x﹣2），
移项，得：2（x﹣2）2﹣（x+2）（x﹣2）=0，
（x﹣2）[2（x﹣2）﹣（x+2）]=0，
（x﹣2）（x﹣6）=0，
则x﹣2=0或x﹣6=0，
则方程的解是：x1=2，x2=6．