问题
填空题
△ABC的三个角A<B<C,且2B=A+C,最大边为最小边的2倍,则三内角之比为 .
答案
1:2:3
2B=A+C，又A+B+C=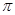
，可得B=
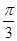，则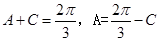
;A<B<C则对应边a<b<c,可得c=2a，由正弦定理可得sinC=2sinA,即
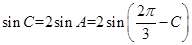，解得C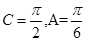
，所以三内角之比为1:2:3.
搜题请搜索小程序“爱下问搜题”
△ABC的三个角A<B<C,且2B=A+C,最大边为最小边的2倍,则三内角之比为 .
1:2:3
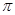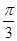2B=A+C，又A+B+C=，可得B=，则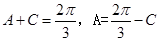;A<B<C则对应边a<b<c,可得c=2a，由正弦定理可得sinC=2sinA,即 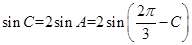，解得C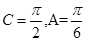，所以三内角之比为1:2:3.