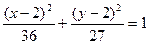问题
解答题
已知一动圆与圆C1: x2+y2+2x-4y+1=0外切，并且和定圆C2: x2+y2-10x-4y-71=0内切，求动圆圆心的的轨迹方程。
答案
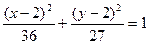
圆C1的圆心为O1(-1,2),r1=2,圆C2的圆心为O2(5,2)，r2=10
设动圆圆心为G(x,y)，则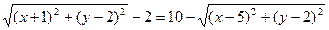
整理得: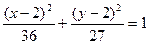
搜题请搜索小程序“爱下问搜题”
已知一动圆与圆C1: x2+y2+2x-4y+1=0外切，并且和定圆C2: x2+y2-10x-4y-71=0内切，求动圆圆心的的轨迹方程。
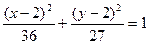
圆C1的圆心为O1(-1,2),r1=2,圆C2的圆心为O2(5,2)，r2=10
设动圆圆心为G(x,y)，则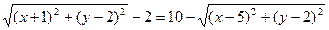
整理得: