问题
解答题
在△ABC中,内角A,B,C的对边分别为a,b,c,且满足 (a-c)cosB=bcosC.
(1)求角B的大小;(2)若b=,求△ABC面积的最大值.
答案
(1)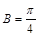 ;(2)
;(2)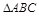 面积的最大值为
面积的最大值为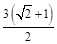 .
.
题目分析:(1)首先利用正弦定理将式子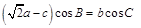 边化为角,化为只含有角的式子
边化为角,化为只含有角的式子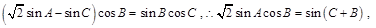 再利用三角形内角和定理及诱导公式即可求得角
再利用三角形内角和定理及诱导公式即可求得角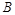 的大小(可以利用余弦定理把角化为边来求得角
的大小(可以利用余弦定理把角化为边来求得角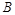 的大小);(2) 根据余弦定理
的大小);(2) 根据余弦定理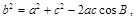 可得
可得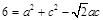 .由基本不等式可得
.由基本不等式可得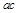 的范围,再利用三角形面积公式
的范围,再利用三角形面积公式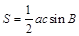 即可求得
即可求得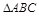 面积的最大值.
面积的最大值.
试题解析:(1) 根据正弦定理有 即
即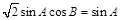 .
.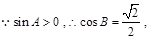 即
即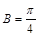 .(可以利用余弦定理把角化为边也可酌情给分)
.(可以利用余弦定理把角化为边也可酌情给分)
(2)根据余弦定理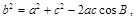 可得
可得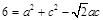 .由基本不等式可知
.由基本不等式可知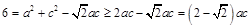 ,即
,即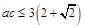 ,故
,故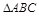 的面积
的面积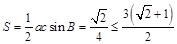 ,即当
,即当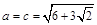 时,
时,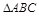 的最大值为
的最大值为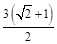 .(另解:可利用圆内接三角形,底边一定,当高经过圆心时面积最大).
.(另解:可利用圆内接三角形,底边一定,当高经过圆心时面积最大).
