问题
填空题
梯形ABCD中,AD∥BC,AB=CD,∠B=60°,若AD=2,BC=6,则AB=______.
答案
如图,过点A作AE∥CD交BC于E,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴AD=CE,AE=CD,
∵AD=2,BC=6,
∴BE=BC-CE=6-2=4,
∵AB=CD,
∴AB=AE,
又∵∠B=60°,
∴△ABE是等边三角形,
∴AB=BE=4.
故答案为:4.
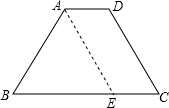
梯形ABCD中,AD∥BC,AB=CD,∠B=60°,若AD=2,BC=6,则AB=______.
如图,过点A作AE∥CD交BC于E,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴AD=CE,AE=CD,
∵AD=2,BC=6,
∴BE=BC-CE=6-2=4,
∵AB=CD,
∴AB=AE,
又∵∠B=60°,
∴△ABE是等边三角形,
∴AB=BE=4.
故答案为:4.
