问题
选择题
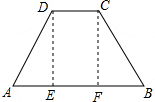
等腰梯形ABCD中,AB∥DC,AD=DC=10,∠DAB=60°,则此梯形的面积等于( )
|
答案
过点D作DE⊥AB于点E,过点C作CF⊥AB于点F,
∴DE∥CF,
∵等腰梯形ABCD中,AB∥DC,
∴四边形CDEF是平行四边形,AD=BC=10,
∴EF=CD=10,
∵∠DAB=60°,
∴∠A=∠B=60°,
∴∠ADE=∠BCF=30°,
∴AE=
AD=5,BF=1 2
BC=5,1 2
∴AB=AE+EF+BF=5+10+5=20,DE=
=5AD2-AE2
,3
∴S梯形ABCD=
(CD+AB)•DE=1 2
×(10+20)×51 2
=753
.3
故选C.