问题
解答题
已知方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0(t∈R)表示的图是圆.
(1)求t的取值范围;
(2)求其中面积最大的圆的方程;
(3)若点P(3,4t2)恒在所给圆内,求t的取值范围.
答案
(1)
.
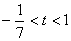(2)圆的方程是
(3)
.
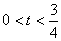(1)已知方程可化为(x-t-3)2+(y+1-4t2)2=(t+3)2+(1-4t2)2-16t4-9,
∴r2=-7t2+6t+1＞0.
即7t2-6t-1＜0,
解得.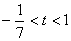
(2)
.
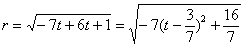当
时,
,此时圆的面积最大,
对应的圆的方程是.
(3)当且仅当t2+1＜-7t2+6t+1时,点P恒在圆内,∴8t2-6t＜0,即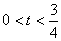.