问题
填空题
若函数f(x)同时满足:①对于定义域上的任意x,恒有f(x)+f(-x)=0; ②对于定义域上的任意x1,x2,当x1≠x2时,恒有
(1)f(x)=
(2)f(x)=x2 (3)f(x)=
(4)f(x)=
能被称为“理想函数”的有______(填相应的序号). |
答案
依题意,性质①反映函数f(x)为定义域上的奇函数,性质②反映函数f(x)为定义域上的单调减函数,
(1)f(x)=
为定义域上的奇函数,但不是定义域上的单调减函数,其单调区间为(-∞,0),(0,+∞),故排除(1);1 x
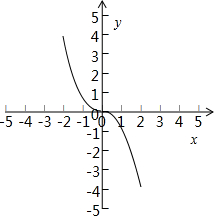
(2)f(x)=x2 为定义域上的偶函数,排除(2);
(3)f(x)=
=1-2x-1 2x+1
,定义域为R,由于y=2x+1在R上为增函数,故函数f(x)为R上的增函数,排除(3);2 2x+1
(4)f(x)=
的图象如图:显然此函数为奇函数,且在定义域上为减函数,故(4)为理想函数-x2 x≥0 x2 x<0
故答案为 (4)
