参考答案：C

解析：

若q=1，则有S₃=3a₁，S₆=6a₁，S₉=9a₁

但a₁≠0，即得S₃+S₆≠2S₉，与题设矛盾，故q≠1。

又依题意得S₃+S₆=2S₉，可得

整理，得q³(2q⁶-q³-1)=0，由q≠0，得方程2q⁶-q³-1=0

即(2q³+1)(q³-1)=0，因为q≠1，q³-1≠0，故

故正确答案为C。

注意：(1)要时刻注意公比q的取值范围，方能不断地简化计算。

(2)复数不能扩展到数列中，而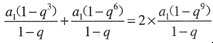只有一个实数解。