Dear Dean,
It is my understanding that this college has received a large donation to be used to improve the quality of life for students: expand the bookstore or add computers to the lab. I strongly argue in favor of the addition of more computers.
We have to think about a greater goal and a more practical way to enhance the quality of life for students. Do we want our college to be known as a place with a great bookstore where you can find CDs and gifts, or as a place where the students can research in their field using the best tools provided by technology?
As a learning institution, this college has the responsibility to offer its students the best technology to help them prepare for their future, since many students will be expected to be familiar with the latest software and other tools when they go on to work.
While they are in college, students find they are expected to use computers. They are asked to create PowerPoint presentations and research many topics on the Internet. Being able to do projects using the computer also gives students the opportunity to find information that without a computer would be much more difficult to find. Since students are competing for good grades, those who have limited access to computers are at a great disadvantage.
If there are more new and faster computers accessible, students will be able to complete their work more efficiently. No more will they have to wait in line, paper and disk in hand, while scanning the room for an empty chair and computer. No longer will they have to sit and wait while an outdated computer struggles to follow their commands.
The more computers are used in society, the more colleges will depend on them as a tool of teaching and learning. Making computers more accessible to students
facilitates their learning process by making it much easier and more engaging(专注), and eventually improves their quality of life.
小题1:The purpose of the author in writing the passage is________.
| A.to explain why students are in great need of computers |
| B.to tell us what benefits students can gain from computers |
| C.to persuade the Dean to purchase more advanced computers |
| D.to describe the problems caused by lack of computers |
小题2:The author mainly wants to tell us in paragraph four that ________.
| A.computers are beneficial to students’ academic success |
| B.computers are the only access to good grades for students |
| C.students find it convenient to do homework by computers |
| D.students wish to use more money to buy more computers |
小题3:The underlined word “facilitates” can be replaced by________.
| A.furthers | B.equips | C.predicts | D.troubles |
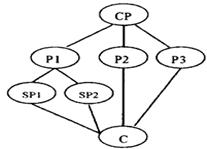
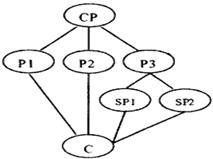
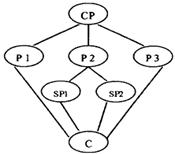
小题4:Which of the following shows the structure of the passage?
CP: Central point P: Point SP: Sub-point(次要点) C: Conclusion