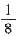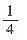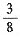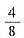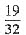已知函数f(x)=x|x-2|.
(Ⅰ)写出f(x)的单调区间;
(Ⅱ)解不等式f(x)<3;
(Ⅲ)设0<a≤2,求f(x)在[0,a]上的最大值.
(1)函数f(x)=x|x-2|=x2-2x=(x-1)2-1 x≥2 -x2+2x=-(x-1)2+1 x<2
∴f(x)的单调增区间是(-∞,1]和[2,+∞);单调减区间是[1,2].
(2)f(x)<3,即 x|x-2|<3,∴
或x≤2 x2-2x -3<0
,x<2 x2-2x+3>0
∴2≤x<3 或 x<2∴不等式f(x)<3的解集为{x|2≤x<3 或 x<2 }.
(3) 当0<a1 时,f(x)是[0,a]上的增函数,此时f(x)在[0,a]上的
上的最大值是 f(a)=a(2-a).
.当1<a≤2 时,f(x)在[0,1]上是增函数,在[1,a]上是减函数,此时,
此时f(x)在[0,a]上的上的最大值是 f(1)=1.
综上,当0<a1 时,此时f(x)在[0,a]上的 上的最大值是 f(a)=a(2-a).
当1<a≤2 时,f(x)在[0,a]上的 上的最大值是1.

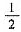 ,他闯关成功的概率为()
,他闯关成功的概率为()