参考答案：B

解析： 由题干关键信息“这两种设备均需要逐次按序经过两条装配线进行装配”和“第一装配线和第二装配线同时接通电源，且连续工作”可知，甲(或乙)设备需要先经过第一装配线进行装配之后，再进入第二装配线进行装配。为了缩短总工时，应适当安排甲、乙两种设备的装配顺序，以缩短第二装配线最后的加工时间(第一装配线完工后还需要用第二装配线的装配时间)，并缩短第一装配线最先的加工时间(第二装配线启动前需要等待的时间)。因此应采取如下原则来安排各设备的装配顺序：在给定的工时表中找出最小值，如果它是第二装配线时间，则该设备应最后加工；如果它是第一装配线时间，则该设备应最先加工。除去该设备后，再按此原则继续进行安排。
在表4—2中，最小台时为1小时，这是乙设备所用的第二装配线装配时间，因此有一台乙设备应放在最后加工；表4—2中除去1小时之后，最小台时为2小时，这是甲设备所需的第一装配线装配时间，因此有一台甲设备应最先加工。
设x₁、x₂分别表示每周甲、乙两种主要设备的产量，则可得到表4—10所示的求解过程。

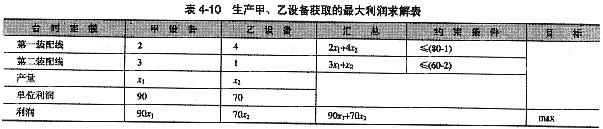
表4—10反映了该生产计划问题可用数学模型表示如下。
目标函数：max z=9x1+7x₂
约束条件：2x₁+4x₂≤(80-1)；3x₁+x₂≤(60-2)；x₁、x₂≥0
求解以上约束条件可得，19.3≥x₁≥15.3，0≤x₂≤12.1。由于现实中设备台数只能为整数，因此求解结果为：19≥x₁≥16，0≤x₂≤12。
在表4-2中，由于生产一台甲设备可获利90万元，而生产一台乙设备可获利70万元，90＞70，因此在条件许可的情况下，为获得最大利润应尽可能多安排甲设备的生产。用图解法按图4-7(包含但不限于此排列方式)所示安排甲、乙设备的生产，可获得最大利润max z=90x₁+70x₂=90×17+70×6=1950万元。在图4-7中，第一装配线总的工作时间为58小时(不包括最后一台乙设备在第二装配线的装配时间1小时)，第二装配线总的工作时间为59小时(包括启动前的等待时间2小时)。