某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
解:(1)设购买1块电子白板需要x元,一台笔记本电脑需要y元,
由题意得: ,
,
解得: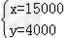 .
.
答:购买1块电子白板需要15000元,一台笔记本电脑需要4000元.
(2)设购买购买电子白板a块,则购买笔记本电脑(396﹣a)台,由题意得: ,
,
解得:99≤a≤101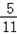 ,
,
∵a为正数,
∴a=99,100,101,
则电脑依次买:297台,296台,295台.
因此该校有三种购买方案:方案一:购买笔记本电脑295台,则购买电子白板101块;
方案二:购买笔记本电脑296台,则购买电子白板100块;
方案一:购买笔记本电脑297台,则购买电子白板99块.
(3)解法一:购买笔记本电脑和电子白板的总费用为:
方案一:295×4000+101×15000=2695000(元)
方案一:296×4000+100×15000=2684000(元)
方案一:297×4000+99×15000=2673000(元)
因此,方案三最省钱,按这种方案共需费用2673000元.
解法二:设购买笔记本电脑数为z台,购买笔记本电脑和电子白板的总费用为W元,
则W=4000z+15000(396﹣z)=﹣11000z+5940000,
∵W随z的增大而减小,∴当z=297时,W有最小值=2673000(元)
因此,当购买笔记本电脑297台、购买电子白板99块时,最省钱,这时共需费用2673000元.
