问题
解答题
已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件: ①AC⊥BD;②AC平分对角线BD;③AD∥BC;④∠OAD=∠ODA。请你以其中的三个条件作为命题的题设,以“四边形ABCD为菱形”作为命题的结论。
(1)写出一个真命题,并证明;
(2)写出一个假命题,并举出一个反例说明。
答案
解:(1)如:若AC⊥BD,AC平分线段BD,AD∥BC,则四边形ABCD是菱形。
证明:如图,设AC与BD交于上点O。
∵AC平分BD
∴BO=DO
又AC⊥BD
∴△ABO≌△ADO
∴AB=AD,∠ABD=∠ADB
同理可知BC=CD
∵AD∥BC
∴∠ADB=∠DBC
∴∠ABO=∠CBO
∴△ABO≌△CBO
∴AB=BC
∴AB=BC=CD=AD
∴四边形ABCD是菱形。(答案不唯一)
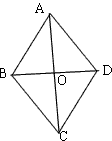
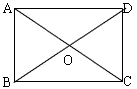
(2)如:若AC平分BD,AD∥BC,∠OAD=∠ODA,则四边形ABCD是菱形
反例:如图,四边形ABCD为矩形。(答案不唯一)
单项选择题
