参考答案：D

解析：
本题考查的知识点为一阶微分方程的求解．
可以将方程认作可分离变量方程；也可以将方程认作一阶线性微分方程；还可以仿二阶线性常系数齐次微分方程，并作为特例求解．
解法1 将方程认作可分离变量方程．
分离变量

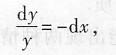
两端分别积分

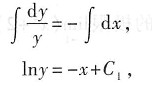
或 y=Ce^-x．
解法2 将方程认作一阶线性微分方程．由通解公式可得

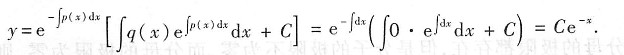
解法3 认作二阶常系数线性齐次微分方程特例求解：
特征方程为r+1=0，
特征根为 r=-1，
方程通解为 y=Ce^-x．