问题
单项选择题
设∫f（x）dx=x2+c，则
=().
A．1
B．-1
C．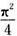
D．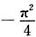
答案
参考答案：B
解析：
本题考查了定积分的换元积分法的知识点．
由∫f(x)dx=x2+C，知∫f(-sinx)cosxdx=∫f(-sinx)dsinx=-∫f(-sinx)d(-sinx)=-(-sinx)2+C=-sin2x+C．
所以
搜题请搜索小程序“爱下问搜题”
设∫f（x）dx=x2+c，则=().
A．1
B．-1
C．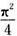
D．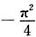
参考答案：B
解析：
本题考查了定积分的换元积分法的知识点．
由∫f(x)dx=x2+C，知∫f(-sinx)cosxdx=∫f(-sinx)dsinx=-∫f(-sinx)d(-sinx)=-(-sinx)2+C=-sin2x+C．
所以