问题
单项选择题
设an),bn,cn均为非负数列,且lima=0,limb=1,limc=∞,则必有______.
A.an<bn对任意n成立
B.bn<cn对任意n成立
C.极限
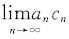 不存在
不存在
D.极限
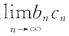 不存在
不存在
答案
参考答案:D
解析:[考点提示] 数列极限.
[解题分析] A,B显然不对,因为内数列极限的不等式性质只能得出数列“当”充分大时”的情况,不可能得出“对任意n成立”的性质.
C也明显不对,因为“无穷小·无穷大”是未定型,极限可能存在也可能不存在.
故应选D.
[点评] D项成立也是明显的,因为极限[*]不是未定式,结论是确定的:[*]∞.应当知道,当[*]
关于∞的确定型还有:(±∞)+(±∞)=(±∞),∞·∞=∞,∞±(有界)=∞;但注意:∞·(有界)不一定为∞.
