问题
单项选择题
函数f(x)在x=1处连续,且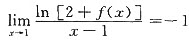 ,则下列说法正确的是()。
,则下列说法正确的是()。
A.f(1)=0
B.f’(1)=0
C.f’(1)=-1
D.f’(1)不存在
答案
参考答案:C
解析:
由 得
得
分母:x→1,分母x-1→0,从而推出分子的极限也必为0。
从而2+f(1)=1,故f(1)=-1,排除A。
再根据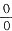 类型,由洛必达法则得
类型,由洛必达法则得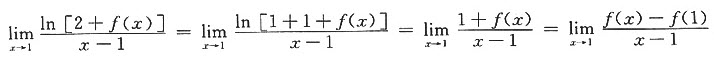 =f’(1),则f’(1)=-1,选C。
=f’(1),则f’(1)=-1,选C。
函数f(x)在x=1处连续,且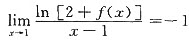 ,则下列说法正确的是()。
,则下列说法正确的是()。
A.f(1)=0
B.f’(1)=0
C.f’(1)=-1
D.f’(1)不存在
参考答案:C
解析:
由 得
得
分母:x→1,分母x-1→0,从而推出分子的极限也必为0。
从而2+f(1)=1,故f(1)=-1,排除A。
再根据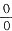 类型,由洛必达法则得
类型,由洛必达法则得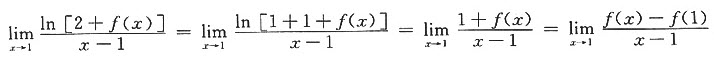 =f’(1),则f’(1)=-1,选C。
=f’(1),则f’(1)=-1,选C。