问题
解答题
如图,平行四边形ABCD中,EF过AC的中点O,与边AD、BC分别相交于点E、F.
(1)试判断四边形AECF的形状,并说明理由.
(2)若EF⊥AC,试判断四边形AECF的形状,并说明理由.
(3)请添加一个EF与AC满足的条件,使四边形AECF是矩形,并说明理由.
答案
解:(1)四边形AECF的形状是平行四边形,
理由是:∵平行四边形ABCD,
∴AD∥BC,
∴∠DAO=∠ACF,∠AEO=∠CFO,
在△AEO和△CFO中
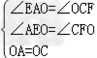
∴△AEO≌△CFO,
∴OE=OF,
∵OA=AO,
∴四边形AECF是平行四边形,
(2)四边形AECF是菱形,
理由是:由(1)知四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形.
(3)添加条件:EF=AC,
理由是:由(1)知四边形AECF是平行四边形,
∵EF=AC,
∴四边形AECF是矩形.
