问题
单项选择题
设f(x)在x=0处存在4阶导数，又设
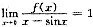．则 ( )．
答案
参考答案：C
解析：
[分析]： 由于[*]，所以当x→0时[*]．于是[*]，即[*](当x→0)．另一方面，由于f(x)在x=0处存在4阶导数，由佩亚诺余项泰勒公式展开到o(x4)，有
[*]
推知f(0)=0，f'(0)=0，f"(0)=0，f"(0)=1，f(4)(0)任意，选(C)．
[注] 推知[*]之后，也可用洛必达法则．