问题
选择题
设f1（x）=|x-1|，f2（x）=-x2+6x-5，函数g（x）是这样定义的：当f1（x）≥f2（x）时，g（x）=f1（x），当f1（x）＜f2（x）时，g（x）=f2（x），若方程g（x）=a有四个不同的实数解，则实数a的取值范围是（ ）
|
答案
解：f1（x）=|x-1|，f2（x）=-x2+6x-5的图象如图，
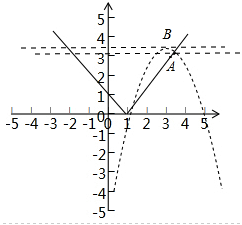
函数g（x）的图象为两函数中位置在上的部分，
即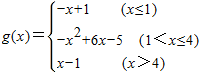
由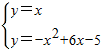
得A（4，3），
f2（x）=-x2+6x-5的顶点坐标为B（3，4）要使方程g（x）=a有四个不同的实数解，
即函数g（x）的图象与函数y=a的图象有四个不同交点数形结合可得3＜a＜4
故选D