问题
单项选择题
设函数f（x）可导，且f（0）=1，f’（-lnx）=x，则f（1）=（）。
A．2-e-1
B．1-e-1
C．1+e-1
D．e-1
答案
参考答案：A
解析：
f’(-lnx)=x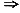
f’(-lnx)=
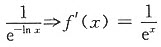，从而f(x)=c-e-x，又f(0)=1，则c=2，故f(x)=2-e-x，f(1)=2-e-1，选A。
搜题请搜索小程序“爱下问搜题”
设函数f（x）可导，且f（0）=1，f’（-lnx）=x，则f（1）=（）。
A．2-e-1
B．1-e-1
C．1+e-1
D．e-1
参考答案：A
解析：
f’(-lnx)=x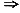f’(-lnx)=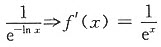，从而f(x)=c-e-x，又f(0)=1，则c=2，故f(x)=2-e-x，f(1)=2-e-1，选A。