问题
单项选择题
设
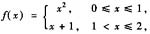 又
又
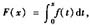 则
则
答案
参考答案:B
解析:[分析一] F(x)是分段函数的变限积分,先求出f(x)
当0≤x≤1时,
[*]
当1
即[*]
于是[*]
因此选(B)。
[分析二] 不必求出F(x),由于
[*]
(f(t)在[0,1]上连续),而
[*]
(f(t)在[1,2]上连续),因此选(B)。
[*]
[*]
设
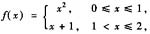 又
又
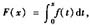 则
则
参考答案:B
解析:[分析一] F(x)是分段函数的变限积分,先求出f(x)
当0≤x≤1时,
[*]
当1
即[*]
于是[*]
因此选(B)。
[分析二] 不必求出F(x),由于
[*]
(f(t)在[0,1]上连续),而
[*]
(f(t)在[1,2]上连续),因此选(B)。
[*]
[*]