问题
单项选择题
设{an}是正数数列，其前n，项的和为Sn，且满足：对一切n∈Z+，an与2的等差中项等于Sn与2的等比中项，则{an}的通项公式为( )。
A．an=n2+n
B．an=n2-n
C．an=3n-1
D．an=4n-2
答案
参考答案：D
解析：
此题可用数学归纳法来证明D成立。
当n=1时，a1=2。设n=k时有ak=4k-2，代入
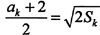，解得Sk=2k2， Sk+1=2k2+ak+1，对n=k+1，由
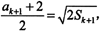因ak+1＞0，
解得ak+1=2+4k=4(k+1)-2。
因此，D对所有正整数都成立。