问题
单项选择题
设A为4×5矩阵，r
A．=4，B为4×2矩阵，则下列命题中不正确的是(A)
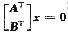只有零解．
B．(A
B)x=0必有无穷多解．
C．
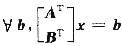有唯一解．
D．
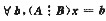必有无穷多解．
答案
参考答案：C
解析：
[分析]： 齐次方程组解的判定问题完全转化为系数矩阵秩的判定，而非齐次线性方程组解的判定，则应考虑系数矩阵的秩与增广矩阵的秩是否相等．注意本题要找的是不正确的命题．
[详解] 因为[*]，由齐次线性方程解的判定知，(A)、(B)两项均成立．
又r(A[*]B[*]b)=r(A[*]B)=4＜7，可见(D)也成立，但[*]与[*]不一定相等，
因此(C)为不正确命题，应选(C)．
[评注] 若r(Am×n)=m，即A为行满秩的矩阵，则r(A)=r(A[*]b)=m，从而Ax=b必有解．
