问题
单项选择题
已知f(x)在(-δ,δ)内具有二阶导数,且
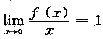 ,f"(x)>0,则
,f"(x)>0,则
答案
参考答案:D
解析:
[分析]: 条件[*]相当于f(0)=0,f'(0)=1,然后用单调性或极值与最值即可导出不等式.
[详解] 由题设[*]知,f(0)=0,f'(0)=1.
令F(x)=f(x)-x,则F'(x)=f'(x)-1,F"(x)=f"(x)>0.
于是F'(x)在(-δ,δ)内单调增加,且F'(0)=0.当x∈(-δ,0)时,F'(x)<F'(0)=0;
当x∈(0,δ)时,F'(x)>F'(0)=0.可见F(x)在点x=0处取极小值,也即最小值,从而有F(x)>F(0)=0,即f(x)>x,x∈(-δ,δ),故选(D).
[评注] 本题也可由泰勒公式,有f(x)=f(0)+f'(0)x+[*]f"(ξ)x2,由f"(x)>0知,当x∈(-δ,δ)时,有f(x)>f(0)+f'(0)x=x.故应选(D)。
