问题
单项选择题
设z=(3x2+y2)xy,则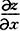 等于().
等于().
A.xy·(3x2+y2)xy-1
B.(3x2+y2)xy·ln(3x2+y2)
C.y·(3x2+y2)xy[(3x2+y2)ln(3x2+y2)+6x2]
D.y·(3x2+y2)xy-1[(3x2+y2)ln(3x2+y2)+6x2]
答案
参考答案:D
解析:
本题考查了二元函数的一阶偏导数的知识点.
因z=(3x2+y2)xy可看作是z=uv,u=3x2+y2,v=xy,复合而成,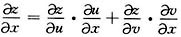 =v·uv-1·6x+uv-lnu·y=xy·(3x2+y2)xy-1·6x+(3x2+y2)xy·ln(3x2+y2)·y=y·(3x2+y2)xy-1·[(3x2+y2)ln(3x2+y2)+6x2].
=v·uv-1·6x+uv-lnu·y=xy·(3x2+y2)xy-1·6x+(3x2+y2)xy·ln(3x2+y2)·y=y·(3x2+y2)xy-1·[(3x2+y2)ln(3x2+y2)+6x2].
