问题
单项选择题
己知三阶矩阵A的3个特征值为λ1=λ2=2，λ3=8，A与特征值2对应的特征向量为α1=(1，-1，0)T，α2=(1，0，-1)T；与8对应的特征向量α3=(1，1，1)T，则A=( )．
答案
参考答案：D
解析：
由于
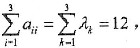(A)、(B)中的矩阵不合题意．
由题意，A应有3个线性无关的特征向量，而(C)中的矩阵，对应于特征值2没有2个线性无关的特征向量．
由排除法，应选(D)．事实上，以A的3个线性无关的特征向量α1，α2，α3为列构造矩阵P，
则
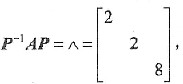故
故选(D)．
